Bài toán tìm đường đi ngắn nhất với giải thuật dijkstra

Với chúng ta sinch viên siêng ngành technology đọc tin, chắc hẳn ko kỳ lạ gì cùng với bài toán thù search đường đi nthêm duy nhất (Shordemo Path Problems) vào thứ thị trọng số nữa. Tại bài viết lần này, bản thân đã làm cho 3 việc:

Giới thiệu bài toán tìm đường đi ngắn tốt nhất cùng vận dụng của chính nó.Giải say đắm lời giải Dijkstra nhằm giải quyết bài xích tân oán trênViết lời giải Dijkstra bằng code Ruby .

Bạn đang xem: Bài toán tìm đường đi ngắn nhất với giải thuật dijkstra

1. Giới thiệu bài xích tân oán search đường đi ngắn thêm nhất

Mình đã chỉ dẫn một ví dụ cơ phiên bản về bài xích toán này.

Bài toán: Cho một đồ dùng thị trọng số bao gồm những nodes A,B,C,D,E,F và khoảng cách thân những nodes khớp ứng với các cạnh nhỏng hình dưới . Tìm đường đi ngắn duy nhất trường đoản cú node B mang đến những node còn sót lại trong đồ gia dụng thị?

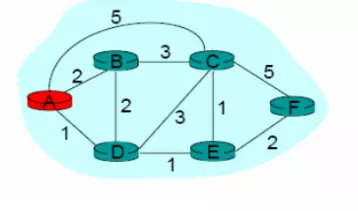
Sau lúc giải bài xích toán thù, ta được hiệu quả nhỏng sau. Đường đi ngắn tuyệt nhất trường đoản cú A đến 5 node còn lại:

Từ A -> B : A - B, tổng độ dài lối đi = 2Từ A -> C : A - C, tổng độ dài đường đi = 5Từ A -> D : A - D, tổng độ nhiều năm lối đi = 1Từ A -> E : A - D - E, tổng độ dài đường đi = 2Từ A -> F : A - D - E - F, tổng độ lâu năm lối đi = 4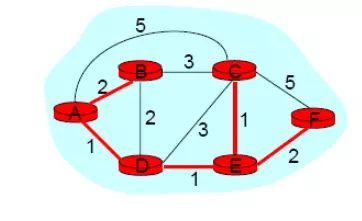

Để nói về áp dụng của Việc giải bài tân oán này, nếu khách hàng gắng các node bằng các giao lộ, cùng những cạnh của chính nó là các tuyến đường, ta đang có một bài bác toán thù hết sức thân thuộc. Bài toán tìm kiếm lối đi nthêm tuyệt nhất mang đến một địa điểm trên bạn dạng đồ gia dụng.

lấy một ví dụ như hình làm việc bên trên, bằng cách xử lý bài xích toán này, các bạn sẽ kiếm được lộ trình nlắp nhất để đi trường đoản cú địa chỉ của công ty mang lại Mễ Trì Thượng.

Bên cạnh đó, nếu gắng những node bởi những router mạng hoặc các host , chúng ta tất cả bài xích toán định tuyến đường đi của một khối hệ thống mạng - loại bài bác tân oán cơ bản cơ mà các kỹ sư mạng nên biết đến:

Có khá nhiều giải thuật được đưa ra nhằm giải quyết và xử lý bài xích toán thù này : Dijkstra"s algorithm , Bellman–Ford algorithm, A* search algorithm, Floyd–Warshall algorithm, .....

Tuy nhiên ngơi nghỉ nội dung bài viết này, mình sẽ phân tích và lý giải về giải thuật Dijkstra cùng cách để viết nó bằng code Ruby.

2. Giải ham mê về giải thuật Dijkstra

Mô tả về giải thuật Dijkstra:

Cách 1: Chọn S = là tập những soure_node bao gồm current_node và passed_node . Với current_node là node đang được xét mang đến, passed_node là những node đã làm được xét.current_node thứ nhất đã là node đích của bài bác tân oán tìm kiếm đường đi nđính thêm độc nhất vô nhị.

Xem thêm: Nhà Gác Lửng Đẹp 5X17 Kiểu Thái Chỉ Với 450 Triệu, Các Mẫu Cầu Thang Gác Lửng Đẹp Nhất Hiện Nay

Cách 2: Khởi tạo lời giải với current_node là node đích với cost(N) là quý hiếm của đường đi nlắp độc nhất vô nhị trường đoản cú N mang đến node đích.Bước 3: Xét các node kề N với current_node . Call d(current_node,N) là khoảng cách thân node kề N và current_node . Với p = d(current_node,N) + cost (current_node). Nếu p thì cost(N) = p . Nếu không thì cost(N) giữ nguyên cực hiếm .Bước 4: Sau Khi xét hết các node kề N, khắc ghi current_node thành passed_node .Cách 5: Tìm current_node new với 2 điều kiện: không hẳn passed_node và cost(current_node) là nhỏ tuổi nhấtBước 6: Nếu tập S = cất đầy đủ các node của thứ thị thì dừng thuật toán. Nếu không thì trở lại Bước 3 .

Để phân tích và lý giải về phong thái giải mã Dijkstra vận động, bản thân đã áp dụng trang bị thị trọng số dưới đây để đi tìm đường đi nthêm duy nhất từ bỏ node C mang lại những node còn sót lại vào thiết bị thị :

Ta cũng khắc ghi current_node (node vẫn xét hiện tại tại) bởi một vệt chấm đỏ trên hình.current_node thứ nhất đã là node đích của bài bác toán thù - sinh hoạt đây là C.

Thuật toán ban đầu chạy bằng phương pháp xét tất cả các node kề với current_node (những node được nối thẳng cùng với current_node ) , sinh sống đây là A, B và D. Ta đang ban đầu với node B trước cùng thực hiện 4 bước:

trước hết ta kiếm được khoảng tầm các trường đoản cú current_node mang đến node B: d(C,B) = 7.Tính toán quý hiếm lối đi từ node đích -> current_node -> node B :p = d(C,B) + cost(current_node) = 0 + 7 = 7Nếu quý giá vừa tính p thì cost(B) = p, trở lại thì cost(B) không thay đổi. ( ở chỗ này 7 đề nghị cost(B) = 7 )Đánh vệt cost(B) lên hình.