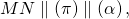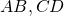Định lý talet trong hình thang
Định lý talet: định lý talet vào tam giác, định lý talet trong hình thang, hệ quả định lý talet, định lý talet trong tam giác vuông, định lý talet trong ko gian…
Đoạn trực tiếp tỉ lệ
Định nghĩa: hai đoạn trực tiếp AB với CD điện thoại tư vấn là tỉ lệ thành phần với nhị đoạn thẳng A’B’ với C’D’ nếu bao gồm tỉ lệ thức
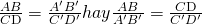
Định lý Talet thuận vào tam giác
Nếu một con đường thẳng song song với 1 cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên nhì cạnh đó phần đông đoạn thẳng khớp ứng tỉ lệ.
Bạn đang xem: Định lý talet trong hình thang
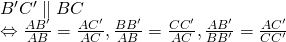
Định lý Talet đảo
Nếu một mặt đường thẳng cắt hai cạnh của một tam giác với định ra trên nhị cạnh này hầu như đoạn thẳng khớp ứng tỉ lệ thì đường thẳng đó tuy nhiên song cùng với cạnh còn sót lại của tam giác. mang lại tam giác ABC nếu:
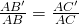
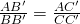
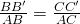
Hệ quả của định lí Talet
Nếu một con đường thẳng cắt hai cạnh (hoặc cắt phần kéo dãn của nhị cạnh) của một tam giác và tuy nhiên song với cạnh còn lại thì nó tạo thành thành một tam giác new có bố cạnh tương xứng tỉ lệ với tía cạnh của tam giác vẫn cho.

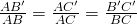
Định lý talet vào hình thang
Nếu một mặt đường thẳng song song với hai đáy của hình thang và cắt hai ở bên cạnh thì nó định ra trên hai sát bên đó gần như đoạn thẳng tương xứng tỉ lệ.
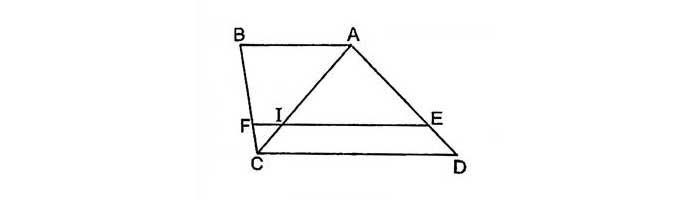
Cho hình thang ABCD, điểm E ở trong AD và F ở trong BC nếu như EF // AB // CD, ta có Ngược lại, nếu: => EF // AB// CD
Định lý talet trong ko gian
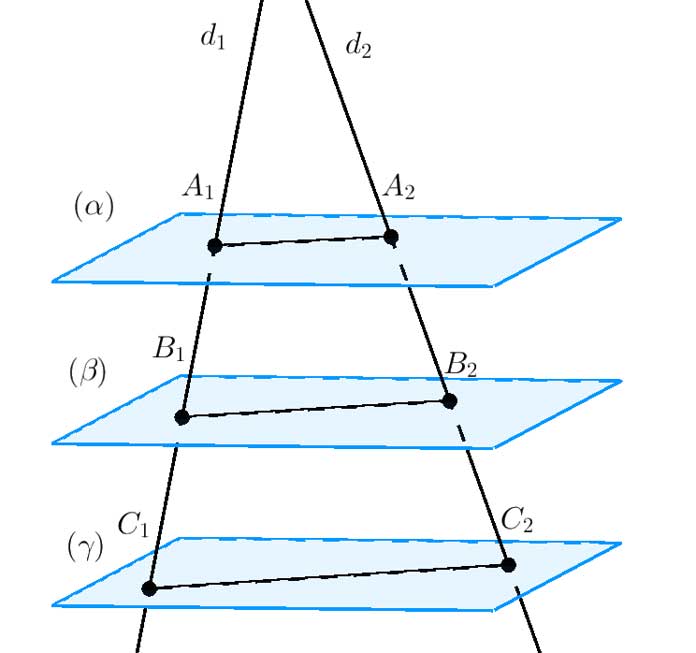
Định lý Thales trong ko gian
Ba khía cạnh phẳng tuy vậy song chắn trên hai tuyến đường thẳng gần như đoạn trực tiếp tỷ lệ.
Xem thêm: Thư Viện Tiền Giang Giới Thiệu Sách: 72 Câu Chuyện Cảm Động Về Mẹ Hay Và Ý Nghĩa
Định lý đảo của định lý Thales trong ko gian
Cho hai tuyến đường thẳng
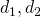
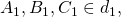
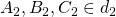
lúc đó những đường trực tiếp
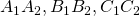
Ví dụ vận dụng định lý talet
Ví dụ 1: đến hình thang ABCD (AB // CD) AB
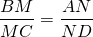
ta suy ra
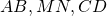
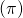
Ta lựa chọn mặt phẳng chứa
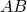
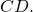
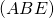
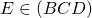
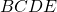
Khi đó