Các hằng đẳng thức đáng nhớ mở rộng

7 hằng đẳng thức đáng đừng quên những đẳng thức cơ phiên bản được chứng tỏ bằng phép nhân nhiều thức với nhiều thức, được sử dụng thường xuyên để giải phương trình, nhân chia các đa thức… Trong bài viết dưới đây, kemhamysophie.com để giúp bạn tổng phù hợp 7 hằng đẳng thức đáng nhớ chính xác, không hề thiếu từ cơ bạn dạng tới không ngừng mở rộng nâng cao, cùng mày mò nhé!. 

Tìm phát âm 7 hằng đẳng thức kỷ niệm cơ bản

Trong toán học, hằng đẳng thức đáng nhớ là đông đảo đẳng thức cơ phiên bản được chứng tỏ bằng phép nhân đa thức với đa thức. đầy đủ đẳng thức này được áp dụng thường xuyên trong các bài toán tương quan đến giải phương trình, nhân chia các đa thức, biến hóa biểu thức tại cấp cho học trung học đại lý và trung học tập phổ thông.

Bạn đang xem: Các hằng đẳng thức đáng nhớ mở rộng

Tóm tắt 7 hằng đẳng thức xứng đáng nhớ 

Trong rất nhiều hằng đẳng thức này, ta tất cả một bên dấu bằng sẽ là tổng hoặc hiệu và bên gọi lại là tích hoặc lũy thừa. Dưới đó là bảng hằng đẳng thức đáng nhớ dành đến bạn:

Bình phương của một tổng	((a+b)^2= a^2+2ab+b^2)
Bình phương của một hiệu	((a-b)^2= a^2-2ab+b^2)
Hiệu hai bình phương	(a^2-b^2=(a+b)(a-b))
Lập phương của một tổng	((a+b)^3= a^3+3a^2b +3ab^2+b^3)
Lập phương của một hiệu	((a-b)^3= a^3-3a^2b +3ab^2-b^3)
Tổng nhị lập phương	(a^3+b^3=(a+b)(a^2-ab+b^2))
Hiệu nhì lập phương	(a^3-b^3=(a-b)(a^2+ab+b^2))

Phát biểu 7 hằng đẳng thức xứng đáng nhớ bằng lời

1. Bình phương của 1 tổng sẽ bằng bình phương của số thiết bị 1 cùng với nhì lần tích của số trước tiên với số máy hai cùng bình phương số thứ hai

2. Bình phương của một hiệu sẽ bằng bình phương của số lần thứ nhất trừ 2 lần tích số thứ nhất với số thứ 2 cộng với bình phương số thiết bị 2.

3. Hiệu của 2 bình phương sẽ bởi tích của tổng 2 số với hiệu 2 số.

4. Lập phương của một tổng sẽ bằng với lập phương số thứ nhất + 3 lần tích bình phương số trước tiên với số thứ hai + 3 lần tích số đầu tiên với bình phương số thứ 2 + lập phương số lắp thêm 2.

Xem thêm: Hướng Dẫn Sử Dụng Điều Khiển Điều Hòa Daikin 1 Chiều Inverter Ga 32

5. Lập phương của 1 tổng sẽ bởi với lập phương số lần đầu tiên -3 lần tích bình phương số thứ nhất với số thứ 2 + 3 lần tích số thứ nhất với bình phương số thứ hai – lập phương số thứ 2.

6. Tổng hai lập phương sẽ bởi tích thân tổng 2 số cùng với bình phương thiếu của một hiệu.

7. Hiệu của 2 lập phương sẽ bằng với tích thân hiệu hai số với bình phương thiếu của một tổng.

Các hằng đẳng thức mở rộng thường gặp 

Hằng đẳng thức đáng nhớ với hàm bậc 2

((a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc)((a+b-c)^2=a^2+b^2+c^2+2ab-2ac-2bc)((a-b-c)^2=a^2+b^2+c^2-2ab-2ac+2bc)

Hằng đẳng thức lưu niệm với hàm bậc 3

(a^3 + b^3 = (a+b)^3 – 3ab(a + b))(a^3 – b^3 = (a – b)^3 + 3ab(a – b))((a+b+c)^3=a^3+b^3+c^3+3(a+b)(a+c)(b+c))(a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca))((a – b)^3 + (b – c)^3 + (c – a)^3 = 3(a – b)(b – c)(c – a))((a + b)(b + c)(c + a) – 8abc = a(b – c)^2 + b(c – a)^2 + c(a – b)^2)((a + b)(b+c)(c+a) = (a+b+c)(ab+bc+ca)-abc)((a + b)(b + c)(c + a) – 8abc = a(b – c)^2 + b(c – a)^2 + c(a – b)^2)((a + b)(b+c)(c+a) = (a+b+c)(ab+bc+ca)-abc)

Hằng đẳng thức dạng tổng quát

(a^n+b^n=(a+b)(a^n-1-a^n-2b+a^n-3b^2-a^n-4b^3+…+a^2b^n-3-a.b^n-2+b^n-1)) (1) với n là số lẻ thuộc tập N

(a^n – b^n = (a – b)(a^n – 1 + a^n – 2b + a^n – 3b^2 + … + a^2b^n – 3 + ab^n – 2 + b^n – 1 ))

Tìm phát âm nhị thức Newton là gì? 

((a + b)^n = sum_k = 0^nC^k_na^n – kb^k)

Với (a, b epsilon mathbbR, n epsilon mathbbN^*)

Bài tập về 7 hằng đẳng thức xứng đáng nhớ

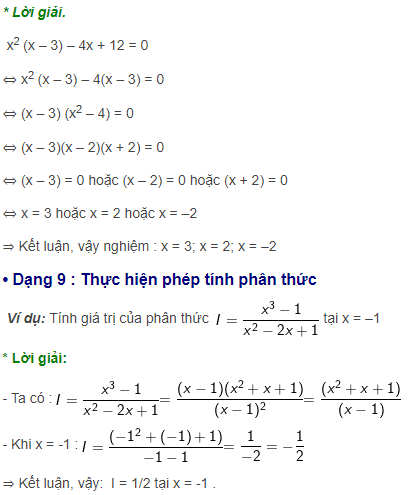
Vận dụng hằng đẳng thức đáng nhớ

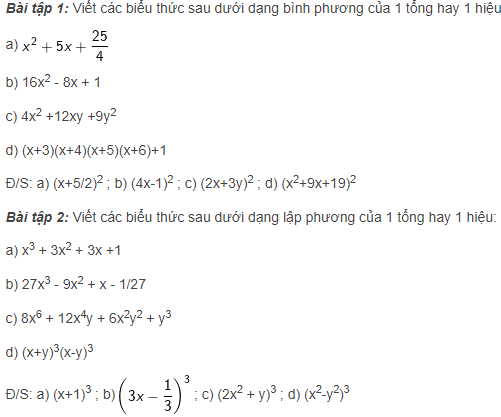
Trên trên đây là bài viết tổng hợp kiến thức về những hằng đẳng thức đáng nhớ cơ bạn dạng và mở rộng. Trường hợp có góp sức hay thắc mắc gì về chủ thể 7 hằng đẳng thức đáng nhớ, chúng ta đừng quên bình luận dưới nhé! Chúc bạn luôn luôn học tốt!.